- Graphical Model 중에서도 큰 부분을 차지하는게 bayesian network!
- 베이지안 네트워크 또한 확률 변수들 사이의 관계를 표현하는 것
Bayesian Network
- A graphical notation of
- Random variables
- Conditional independence
- To obtain a compact representation of the full joint distributions
- Syntax
- A acyclie and directed graph (사이클이 없는 방향성이 있는 graph)
- A set of nodes
- A random variable
- A conditional distribution given its parents
- $P(X_i | Parents(X_i))$
- A set of links
- Direct influence from the parent to the child
Interpretation of Bayesian Network
- Topology of network encodes conditional independence assertions
(네트워크의 구조는 conditional independence를 가정)
-> 충치가 있다는 조건 하에서 구취가 나고 아프다. 날씨는 고통과 구취와는 상관이 없다
- often from the domain experts
- What is related to what and how
- Interpretation
- Weather is independent of the other variables
- Toothache and Stench are conditionally independent given Cavity
- Cavity influences the probability of toothache and stench
내가 이가 아플 확률이 구취가 나면 올라간다. 내가 충치가 없다는 정보를 알고 있는 상황에서는 구취와 충치는 conditional independence한 관계가 되버리므로 관게가 없다!
Components of Bayesian Network
- Qualitative components
- Prior knowledge of causal relations
- Learning from data
- Frequently used structures
- Structural aspects
- Quantitative components
- Conditional probability tables
- Probability distribution assigned to nodes
- Probability computing is related to both
- Quantitative and Qualitative
Bayes Ball Algorithm
- Purpose: checking $X_A \perp X_B|X_C$
- Shade all nodes in $X_C$
- Place balls at each node in $X_A$
- Let the ball rolling on the graph by Bayes ball rules
- Then, ask whether there is any ball reaching $X_B$
- Markov Blanket
- A 라는 특정 random variable이 bayesian network 위에 있다고 가정할 때, A가 다른 random variable이랑 전부 conditional independence가 되게 만들어주는 condition을 찾아보자
- D-Seperation
- X is d-separated(directly separated) from Z given Y if we cannot send a ball from any node in X to any node in Z using the Bayes ball algorithm
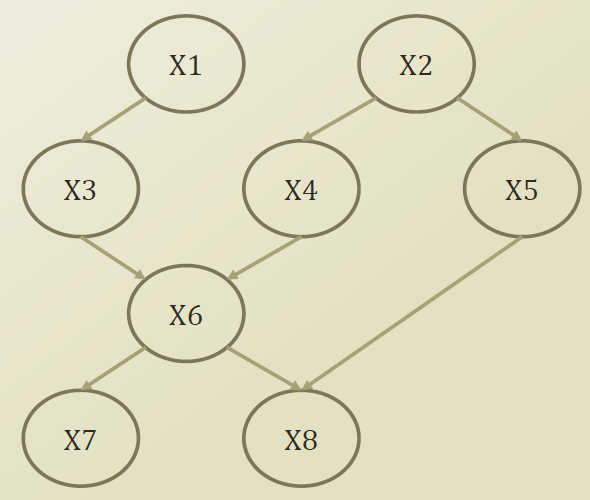
Factorization of Bayesian networks
- $P(X_1, X_2, X_3) = P(X_1 | X2, X3) P(X_2|X_3)P(X_3)$
- (Assume $X_1 \perp X_3 | X_2)$)
= $P(X_1|X_2)$
- Factorizes according to the node given its parents
- $P(X) = \prod_i P(X_i|X_{\pi_i} )$
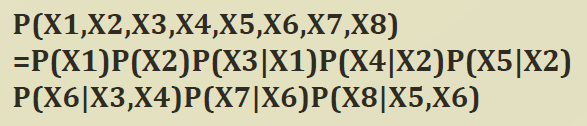
'기계학습 > 인공지능및기계학습개론정리' 카테고리의 다른 글
| Hidden Markov Model (2. For-Backward Prob. Calculation/ Viterbi Decoding Algorithm) (0) | 2020.11.19 |
|---|---|
| Hidden Markov Model(1: Joint, Marginal Probability of HMM) (0) | 2020.11.16 |
| Naive Bayes Classifier + Logistic Regression (parameter approximation) (0) | 2020.08.27 |
| MLE(Maximum Likelihood Estimator) vs MAP(Maximum A Posterior) (0) | 2020.08.27 |
| Logistic Regression + Gaussian Naive Bayes (0) | 2020.08.27 |