분포 정리

가끔씩 다시 보면 생각이 잘 안난다. 맨날 까먹네.

공부가 부족한가보다.

 

 

 

 

 

 

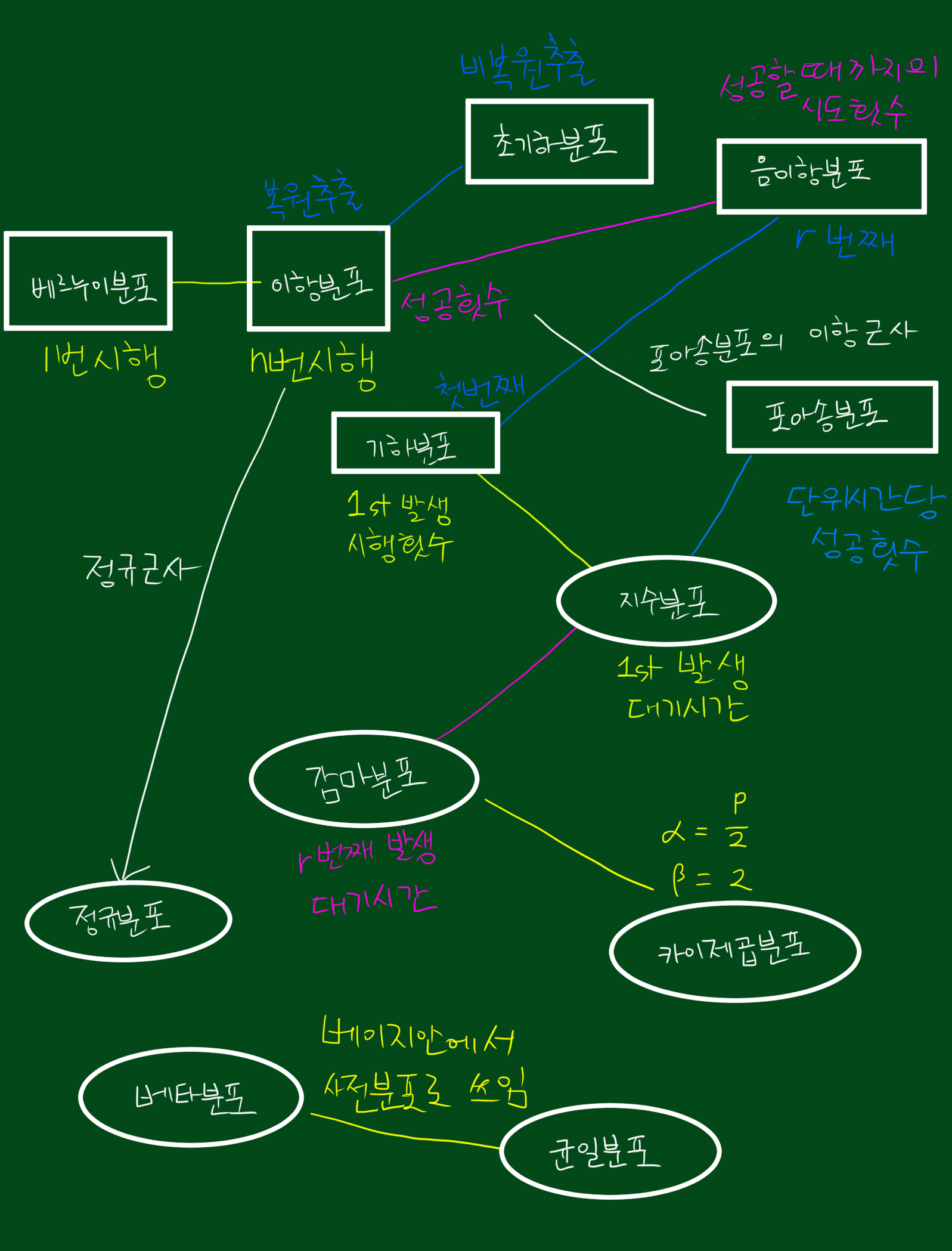
[데이터 사이언스에 많이 사용되는 확률밀도함수들]

- Bernoulli
동전의 앞/뒤처럼 이벤트가 0 또는 1밖에 일어나지 않는 분포를 말합니다. 동전은 확률이 0.5/0.5 겠지만 다른 경우도 있을 수 있겠죠

- Uniform
주사위처럼 모든 결과에 대한 확률이 동일한 확률분포입니다.

- Binomial
동전을 n번 던졌을 때 p번만큼 앞면이 나올 확률은? Binomial은 이렇게 0 또는 1이 나오는 이벤트(각각이 Bernoulli확률을 갖는 이벤트)에 대해 1이 발생활 횟수에 대한 확률입니다.

- Poisson
1시간에 평균 10번의 전화통화가 온다고 해봅시다. 그렇다면 한시간에 12번 전화통화가 올 확률은? 이것이 바로 poisson(포아송) 확률입니다. 이것은, 예를들어, 60분 중 48번의 실패(0)와 12번의 성공(1)을 하면 되겠죠? 또는, 60분이 아니라 더 잘게 쪼개서 988번의 실패와 12번의 성공을 하면 되겠죠? 이처럼 시행횟수가 크고 이벤트가 일어날 확률이 작은 bionomial 분포가 바로 poisson 분포에 수렴합니다. (이 때문에 binomial의 근사로도 쓰이지요.)

- Hypergeometric
까만공과 하얀공이 절반씩 있는데 그것을 여러번 뽑는다고 해보죠. 그럼 이것은 Binomial과 같겠죠? 땡~ 아닙니다. 왜냐면 공을 뽑을 때 만약 그 공을 다시 채워넣지 않는다면 남아있는 공의 확률은 바뀔테니 말이죠. Binomial의 경우와 달리 replacement(다시 보충)를 허용하지 않는 것이 바로 hypergeometric 확률입니다.

- Geometric
주사위를 굴렸을 때 한번에 6이 나올 확률은? 두번만에 6이 나올 확률은? 세번만에, 네번만에... 이처럼 geometric 분포는 어떤 이벤트가 일어날 때까지의 횟수에 대한 확률입니다. 재밌는건 이벤트의 확률이 어떠하든 늘 "가장 첫번째"에 이벤트가 발생할 확률이 가장 크다는 것이죠.

- Negative Binomial
Geometric이 한번 성공할 때까지 걸리는 횟수에 대한 분포라면 negative binominal은 n번 성공할 때까지 걸리는 횟수에 대한 분포입니다. (이름을 왜 geometric이랑 비슷하게 안지은거야?;;)

- Exponential
bionomial의 연속버전이 poisson이었다면, geometric의 연속버전이 exponential분포입니다. 다시말해 "평균 5분만에 전화가 걸려온다고 할 때 다음 전화가 7분 후에 걸려올 확률은?"과 같이요.

- Weibull
exponential이 "다음 이벤트가 성공할 때 까지의 실패구간은"에 대한 함수였다면 반대로 Weibull은 "첫 실패가 발생할 때까지 이번 이벤트가 성공할 구간"에 대한 확률입니다.

- Gaussian (Normal)
너무 유명한 확률분포죠. 특히 매우 많은 수의 동일 확률분포를 가진 샘플들의 산술평균은 그 샘플들이 어떤 분포를 따르든(binomial이든 exponential이든 아님 다른거든) 결국 Gaussian 분포로 수렴한다는 "중심극한정리"가 매우 유용하기에 이 분포는 매우 많은 곳에 적용될 수 있죠.

- Log-normal
변수의 log 값이 Gaussian을 나타내는 분포입니다. 다시말해 Gaussian을 exponential 한 함수지요.

- Student’s t-distribution
정규분포의 mean 값에 대한 판단을 내릴 떄 사용하는 확률분포입니다.

- Chi-squared distribution
Gaussian 분포를 가진 확률변수의 제곱들의 합에 대한 분포입니다. 예를 들어 k자유도의 chi-squared는 k개의 독립적인 Gaussian들에 대한 합의 확률분포죠.